What is Monte Carlo Simulation?

Monte Carlo Simulation is a computer-based mathematical method or technique used in risk analysis and aids in the decision-making process. The technique is employed in areas including engineering, finance, R&D, and energy. It shows the possible consequences of one’s decisions and also evaluates the effect of risk. Thus, the technique helps make improved decisions when there is uncertainty.

Investment projects with significant project value need to be risk analysed before making any decision. The Monte Carlo method allows considering various cost estimation scenarios related to any project affecting the outcome.

Evolution of Monte Carlo Simulation

Monte Carlo simulation was first used around the year 1944. The technique has undergone many changes and evolved over the period. Initially, to use the method, a series of variables were generated to get the desired result. Choosing a large set of random numbers to make the simulation work was time-consuming, and with the advent of the computer, the problem was gradually solved.

Monte Carlo Simulation method uses probability distribution to generate a model using a random or stochastic variable. A wide range of outcomes is generated using the probability distribution of input variables. To model variables such as uniform, normal, or triangular, different probability distributions are implemented.

Monte Carlo Simulation can be used in determining or analysing risks in various stages of project management. The method can be useful in determining risk categories:

• The simulation can analyse different projects of similar or different investment values based on variables associated with the projects. Here project value, execution period, standard deviation values could be used as variables for modelling data.
• Estimation of risk associated with project cost exceeding the initial project value.
• Estimation of risk associated with the project implementation period exceeding the allocated period.

Why has it gained so much ground?

Monte Carlo Simulation provides a far better simulation model of associated risks. The simulation generates multiple outcome scenarios along with the probability of occurrence of each outcome.

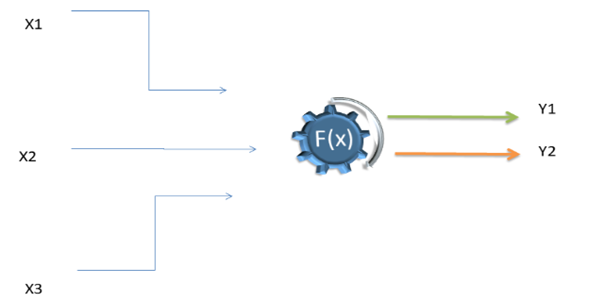
Deterministic Model (Source: Copyright © 2021 Kalkine Media Pty Ltd.)

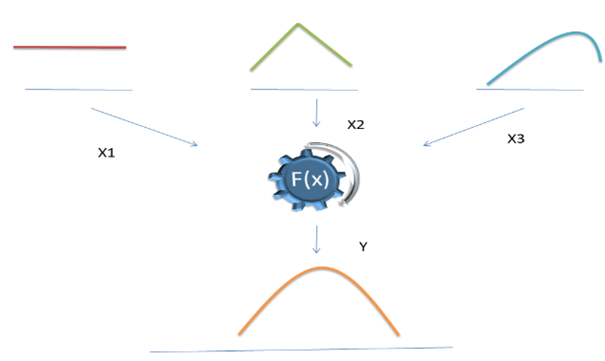
Stochastic Model (Source: Copyright © 2021 Kalkine Media Pty Ltd.)

Explained below are the some of the key features that have made the technique popular:

1. Efficient

Monte Carlo method reduces complex models to a set of basic events and interactions when applied to physical systems. The technique can encode model behaviour through a set of rules that can be proficiently implemented on a computer. This will allow general models to be implemented and studied on a computer than the analytic methods.

Monte Carlo Simulation’s complex algorithms can be broken into pieces and run at a different time or on different processors to save the computing time.

2. Risk Analysis

As mentioned above, Monte Carlo provides not only an outcome but also the probability of occurrence of that outcome. This is a unique feature that can be put to use during chemical or physical research works when a wide variety of variables are available.

For e.g., using the method in subatomic research when the degree of variables like temperature, entropy, energy, velocity, and several other parameters are involved. The ongoing fusion reaction is gaining popularity worldwide. The risk associated with the projects is enormous as far as project financials and overall safety of the project is involved.

3. Sensitivity Analysis

Monte Carlo Simulation determines which variable in the input is going to impact the outcome by most. The analysts even can see which combination of data is impacting the result by what degree.